Алгоритм Максимальный Поток
 Я. Илья
24 мар 2012
Я. Илья
24 мар 2012
Задача:
Найдите величину максимального потока в сети.
Входные данные.
Первая строка входного файла содержит целое число N - количество вершин сети. Вторая строка входного файла содержит целое число M - количество дуг сети. В каждой из следующих M строк содержится ровно три числа a, b, c. Эти числа описывают дугу, идущую из вершины с номером a в вершину с номером b и имеющую пропускную способность c. Последние две строки содержат целые числа s и t - номера вершин, являющихся истоком и стоком, соответственно. Вершины нумеруются последовательными натуральными числами от 1 до N. В сети между фиксированной парой вершин в фиксированном направлении может быть не более одной дуги.
Выходные данные.
Единственная строка выходного файла должна содержать одно целое число, равное величине максимального потока в сети, описанной во входном файле.
Пример.
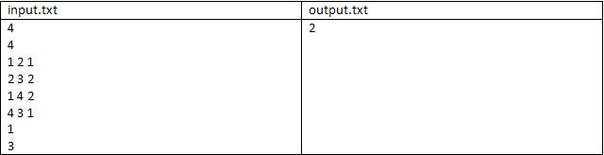
Идея: ![]()
Повторяем, пока не найдём максимальный поток
1. Ищем путь от вершины 1 до вершины n и делаем соответствующие заполнения
2. В специальную переменную суммируем результат потока на каждом шаге
3. Заполняем все «трубы» пути на i-том шаге максимальным потоком на этом шаге
Задача о максимальном потоке заключается в нахождении потока такого, что величина потока максимальна.
Код:
type zap=record pr,dp:longint;end; //для хранения информации о потоке используем записи
var c,f:array[0..900,0..900]of longint; q:array[0..900]of longint; p:array[0..900]of zap;
i,s,t,v,n,m,a,b,d,pot,un,uk,x,y:longint; ud:boolean;
Function min(a,b:longint):longint; //ну тут всё понятно...
begin
if a<b then min:=a
else min:=b;
end;
Procedure PUD; //процедура Поиск Удлиняющей Дуги
begin
un:=1;uk:=2;q[1]:=s; p[s].pr:=s; p[s].dp:=1 shl 30;
while (un<>uk)and(p[t].dp=0) do //повторяем, пока есть куда лить и поток не дошёл до конца
begin
v:=q[un];un:=un+1; //берём из очереди вершину
for i:=1 to n do
if ((c[v,i]>0)or(c[i,v]>0))and(p[i].dp=0) //если из i в v (или наоборот) есть путь и на этом шагу воды не добавляли,...
then if (f[v,i]<c[v,i]) //то если сюда можно протечь,...
then begin
q[uk]:=i;
uk:=uk+1; //то добавляем вершину в очередь
p[i].pr:=v; // предки - это святое
p[i].dp:=min(p[v].dp,c[v,i]-f[v,i]); //выбираем количество воды, которое туда потечёт (сколько текло в v или сколько можно впихнуть)
end
else if f[i,v]>0 then begin //иначе если течёт по обратному ребру,...
q[uk]:=i;
uk:=uk+1; //добавляем вершину в очередь
p[i].pr:=-v; //как я уже говорил, предки - это святое, но чтобы знать, что мы получили жидкость из обратного ребра, делаем ему отрицательный знак
p[i].dp:=min(p[v].dp,f[i,v]); //выбираем количество воды для течения (сколько текло в v или сколько льется)
end;
end;
if p[t].dp=0 then ud:=false; //если ничего не дотекло, значит мы нашли максимальный поток
end;
Procedure VUD(v:longint); //процедура Восстановление Удлиняющей Дуги
begin
if abs(p[v].pr)=v then exit; //если каким-либо образом мы попали из самого себя в себя, то мы в начале
if p[v].pr>0 then f[p[v].pr,v]:=f[p[v].pr,v]+p[t].dp //если есть прямой предок, то добавляем к потоку в трубе предок v и v столько, сколько долилось в последнюю вершину
else if p[v].pr<0 then f[v,-p[v].pr]:=f[v,-p[v].pr]-p[t].dp; //иначе, если есть предок по обратной дуге, то уменьшаем количество воды в трубе v и -предок v на столько, сколько дотекло до последней вершины
VUD(abs(p[v].pr)); //восстановление дуги от предка вершины и соответствующие заполнения
end;
Begin
read(n,m); //ввод данных в соответствующие для них массивы
for i:=1 to m do
begin
read(x,y);
read(c[x,y]);
end;
read(s,t);
ud:=true; //переменная, которая определяет способность пролить воду из первой в последнюю вершину
while ud do //повторяем алгоритм, пока не найдём максимальный поток
begin
for i:=1 to n do //так как мы запускаем процедуры по несколько раз, обнуляем массивы
begin
p[i].pr:=0;
p[i].dp:=0;
end;
PUD;
if ud then begin
pot:=pot+p[t].dp; //переменная, хранящая в себе максимальный поток
VUD(t); //восстанавливаем и заполняем с конца
end;
end;
writeln(pot); //выводим величину максимального потока
End.
 Илья М.
30 мар 2012
Илья М.
30 мар 2012
Процедуры называются "поиск удлиняющей дуги" и "восстановление удлиняющей дуги"
 Илья М.
01 апр 2012
Илья М.
01 апр 2012
Точнее будет сказать что тогда мы не нашли удлиняющую дугу

